ボロノイ図作成ソフト
ボロノイ図
最近、友達からお題をもらったのでボロノイ図作成ソフトを制作してました
ボロノイは幾何学の基本的なテーマの1つらしいのですが
自分には何の知識も無かったので (ボロノイなのかボノロイなのか)
1から仕組みを調べて試行錯誤
2週間くらいかけて、ようやく正常に動作するものが作れました。
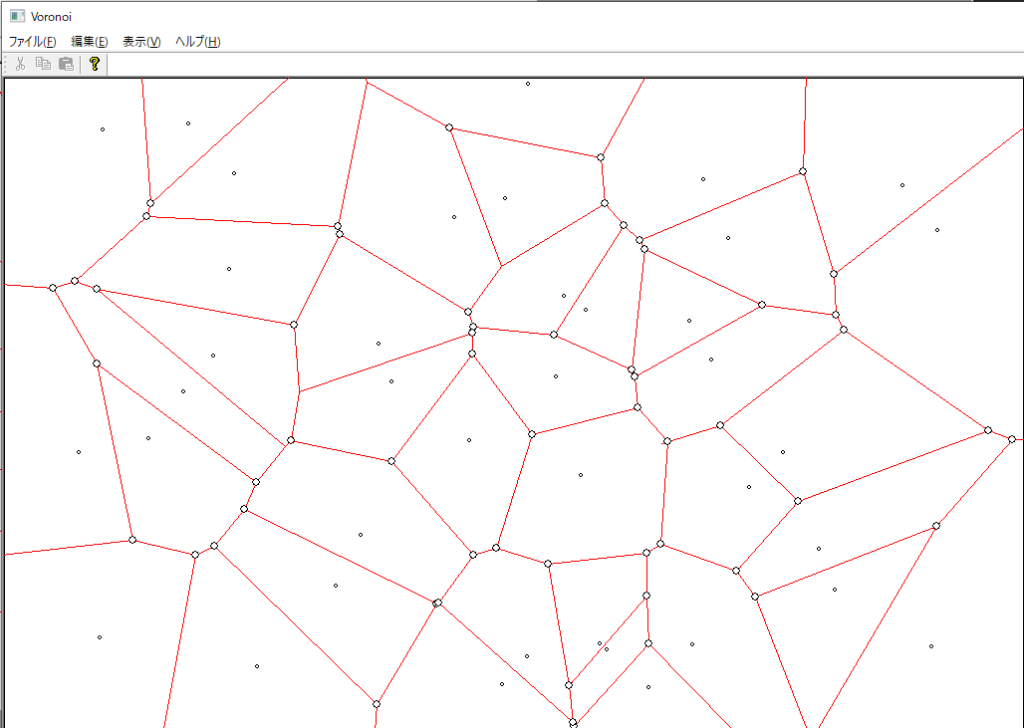
ダブルクリックした位置に母点を設置して、ボロノイ領域を表示するプログラムです
Toolsページにアップしました
ボロノイ図とは置かれた点の垂直二等分線だけで構成された領域
自然界でよく見られる現象らしいです
仕組みを調べる過程でYoutubeの動画を見たんですけど、板の上に絵の具を垂らしてアクリル板を 上から 水平に押し付けるとボロノイの形になるというものがありました
3点間の垂直二等分線が1点で交わるという性質
均等・テリトリー
これらが美観を生み出してるのかな(適当)
意外と複雑
最初は簡単に作れるだろうと思っていたのですが、プログラムにしようとすると意外と難しい
必要な線と不要な線の判別、線の長さの調整、指数的に重くなる処理・・・
制作過程で何度も思考停止しました
自分が考えたボロノイ図の作成手順
1.母点同士を結ぶ線を作成する
2.作成した線を90度回転させる
3.線の長さを延長する
4.1~3を全ての点同士で行う
5.不要な線を削除する
6.線を交点まで短くする
といった感じ
1~4までは簡単に行えたのですが
5と6が難しくて、時間が掛かりました
5の不要な線を削除する処理は
各母点から360本、360度の線を伸ばし”最初に当たった” “自分が作った線“に有効フラグをつけて、それを全ての母点で行い、最終的に有効フラグが付かなかった線を削除するという形を取りました。
もっとスマートな方法があると思うんですけど自分の頭ではこれが限界(汗
次に6の線を交点まで短くする処理ですけど、これにすごく悩みました
最初は5と同じように360本の線を伸ばして、最初に当たった線が自分が作ったもの以外の線だった場合、その線を最初の交点まで縮めるという処理を書きました
かなり重い処理なので、点を50個打っただけでカクつき始めました
それに線に当たらなかった線が残ったりもしました
しばらくして思いついたのが、同じ母点が作った線同士の交点を求めて、母点より外を向いている端2点を
交点まで縮めるという方法
一つの点あたり何百回の当たり判定をしなくて済む画期的な方法でした
どうやって外側か判別すればいいか悩みましたけど、母点から線の両端まで新しい線を伸ばして、線を跨いだら外側になるということに気づいたので、そのとおりに実装
これにより処理は大幅に高速化、200点ほど置いてもカクつかくなりました

これでボロノイ図を表示するプログラムは完成
面積を求める
実用的なソフトにするなら、その領域の面積が求められたら良いなと思い、領域の面積を求める機能を実装しました
多角形の面積を求める方法をネットで調べて
1.どんな多角形も複数の三角形に分割できる
2.三角形の3辺の長さから面積を求めるへロンの公式というものがある
ということが分かりました
各頂点は座標で管理されているので、長さを出すのは簡単です(三平方の定理)
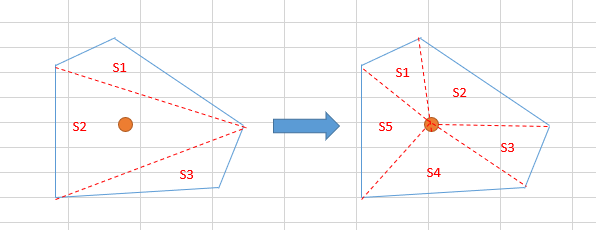
複数の辺で構成される多角形を三角形に分割するという処理は複雑なので
線と母点で構成される三角形の面積を累計加算していくという方法を考えました
それなら線を一回ずつループで回すだけで計算できます
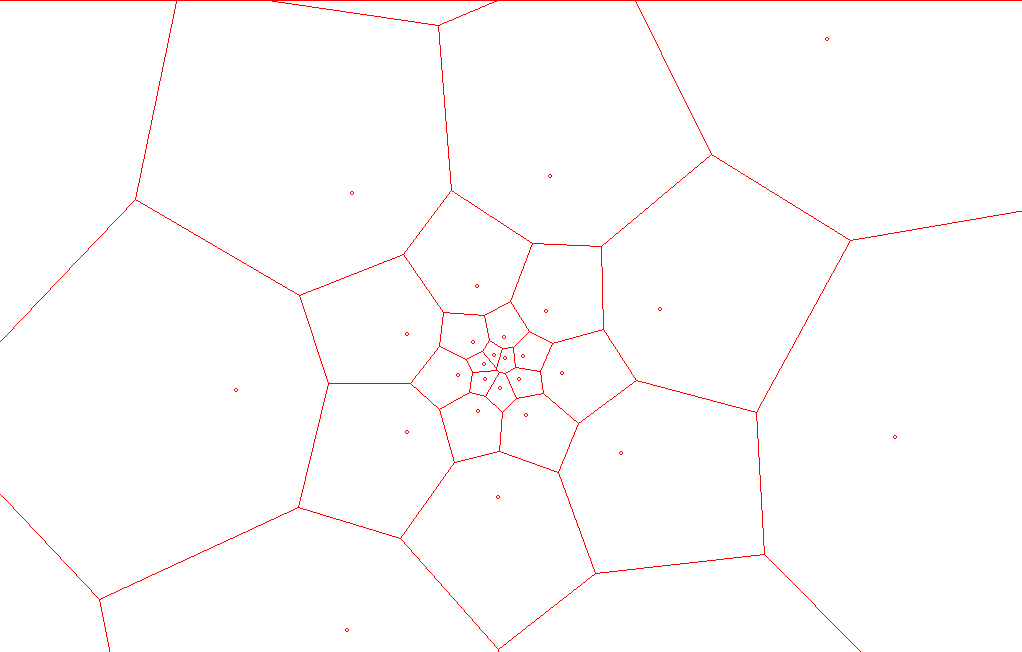
完成したのがこちら

面積はピクセル基準なので、係数を掛ける必要がありますね
おわりに
好奇心から始めた挑戦でしたけど、かなり苦戦しました
苦労したぶん完成したときの達成感は大きかったです
とてもいい勉強になりました
完成したら終わりではなく
ここから思うままに機能を拡張していくのが楽しいんですよね
拡張としては画像ファイルを読み込んでテリトリーの分析なんかに使ったり
例えば、地図のスクリーンショットから店舗の勢力図などを分析して
どの位置にコンビニを置いたら相手の勢力を削りつつ、自分の領域を拡げられるか
みたいな分析ができると思います
どちらが多くの領域を獲得できるかを競うボロノイ碁みたいなゲームも面白そうですね
他にはアートなんかにも使えそう
過去に作った物同士を組み合わせて、どんどん大きな物が作れるようになっていく
それが趣味プログラミングの醍醐味だと思います


最近のコメント